FANTOM

Publications

First order control of syntectonic sedimentation on crustal‐scale structure of mountain belts, Erdos, Z., Huismans, R. S., van der Beek, P., submitted to EPSL
Extensional inheritance and surface processes as controlling factors 2 of mountain belt structure, Z. Erdos, R.S. Huismans, P. van der Beek, and C. Thieulot, accepted in JGR, 2014.
C. Thieulot, P. Steer and R.S. Huismans, Three-dimensional numerical simulations of crustal systems undergoing orogeny and subjected to surface processes, submitted to Geochem. Geophys. Geosyst.
3D numerical modelling of graben interaction and linkage: a case study of the Canyonlands grabens, Utah, V. Allken, R.S. Huismans, Haakon Fossen and C. Thieulot, Basin Research, 25, 1-14, 2013.
Factors controlling the mode of rift interaction in brittle-ductile coupled systems: A 3D numerical study, V. Allken, R.S. Huismans and C. Thieulot, Gcubed 13(5), 2012.
Three-dimensional numerical modeling of upper crustal extensional systems, V. Allken, R.S. Huismans and C. Thieulot, JGR 116, 2011.
FANTOM : two- and three-dimensional numerical modelling of creeping flows for the solution of geological problems, C. Thieulot, Physics of the Earth and Planetary Interiors, 188, 2011

Introduction

FANTOM is a finite element code for the solution of the Stokes and heat transport equations. It has been purposely designed to address geological flow problems in two and three dimensions. A variety of rheologies has been implemented including linear and non-linear thermally activated creep and brittle (or plastic) frictional models. A cloud of particles is used to track materials in the simulation domain which allows to record the integrated history of deformation; its density is variable and dynamically adapted. The solution to the large system of algebraic equations resulting from the finite element discretization and linearization of the set of coupled partial differential equations to be solved is obtained by means of an efficient (sequential or massively parallel) direct solver. The code can be run in sequential or parallel mode.

Three typical simulations illustratring a different version of the code are presented and briefly discussed: the 2D numerical sandbox, a 2D lithospheric extension experiment, and a 3D crustal scale orogeny experiment.

FANTOM2D

In order to test the large deformation viscous-plastic behaviour of the code, the extensional numerical sandbox experiment [1] was carried out with the two-dimensional sequential version of the code. The central idea is to compare analogue experiments observations with numerical results, the former being conducted in several laboratories, the latter obtained with different numerical codes.

We focus here on the extensional setup: this experiment consists of a sand layer which overlies a viscous central layer. A thin rigid sheet covering the base of the model extends from the middle to the right lateral wall and is attached to it. The outward mouvement of the right wall leads to an extensional system. The sand is frictional plastic and characterised by ρ=1560kg/m³, c=10Pa, φ=36^o, φ_sw=31^o, ε₁=0.5, ε₂=1.0. The silicone is a viscous material characterised by ρ=965kg/m³ and μ=5x10⁴Pa.s.

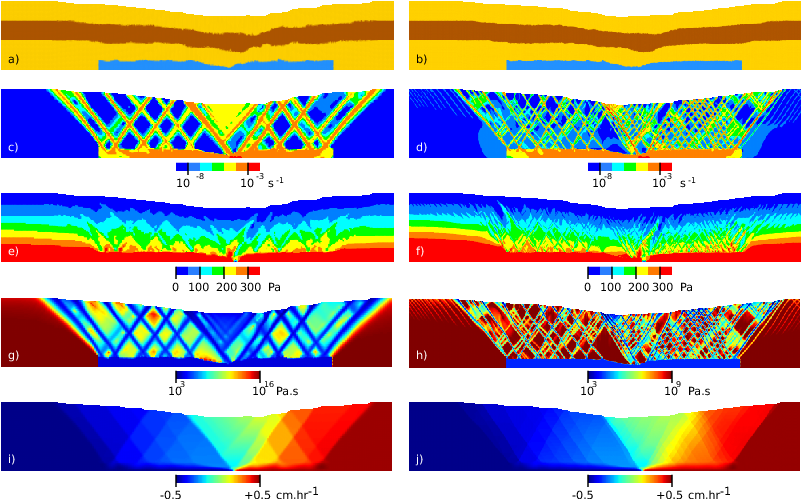
[1] The numerical sandbox: comparison of model results for a shortening and an extension experiment S. Buiter and A.Y. Babeyko and S. Ellis and T.V. Gerya and B.J.P. Kaus and A. Kellner and G. Schreurs and Y. Yamada, Analogue and Numerical Modelling of Crustal-Scale Processes. Geological Society, London. Special Publications, p29-64, 253, 2006.

FANTOM2Dp

This experiment is nearly identical to the one discussed in [2] in which plane strain thermo-mechanical finite-element model experiments have been used to investigate the effects of frictional plastic strain softening and inherited weakness on the style of lithospheric extension.

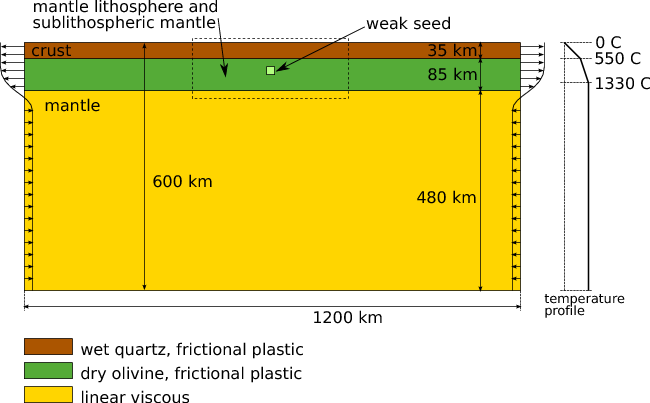
The setup, shown hereunder consists of three layers:

the top layer is the crust, consisting of wet quartz. It is 35km thick and is characterised by a visco-plastic rheology. ρ₀=2800kg/m³, c_qt=20x 10⁶ Pa, n_qt=4.0, Q_qt=223x 10³ J/mol, A_qt=1.10x 10^^-28Pa^-n.s^-1, V_qt=0 m³/mol, φ=7^o, φ_sw=1^o, ε₁=0.5, ε₂=1.5.
the middle layer is the lithosphere and sublithospheric mantle, composed of dry olivine. It is 85km thick and its rheology is also visco-plastic. ρ_₀=3300kg.m^-3$, c_ol=20x 10⁶ Pa, n_ol=3.5, Qol=540x 10³J/mol, A_ol=2.4168x10^-15Pa^-n.s^-1, V_ol=25x 10^-6m^3.mol^-1, φ=7^o, φ_sw=1^o, ε₁=0.5, ε₂=1.5.
the bottom layer is the mantle, characterised by a purely viscous rheology. ρ₀=3300kg/m³, μ=10²¹Pa.s

The size of the numerical domain is Lx=1200km, Ly=600km and the boundary conditions are as follows: the temperature is set to T=1330^o at the base of the model and to 0^o at the top. At startup, a constant geotherm T=550^o is placed at the base of the crust

The extensional velocity applied to the sides of the crust is v_ext=0.5cm/yr and a re-entrant velocity field is applied on the rest of the boundary so as to lead to a zero net-flux through the vertical sides of the box. A weak seed is placed in the upper part of the lithosphere and represents the weakest zone of inherited damage, therefore controlling the strain localisation process.

All materials see their density depend on the temperature field with a thermal expansion coefficient α=3.1x 10^-5 ^oC^-1.

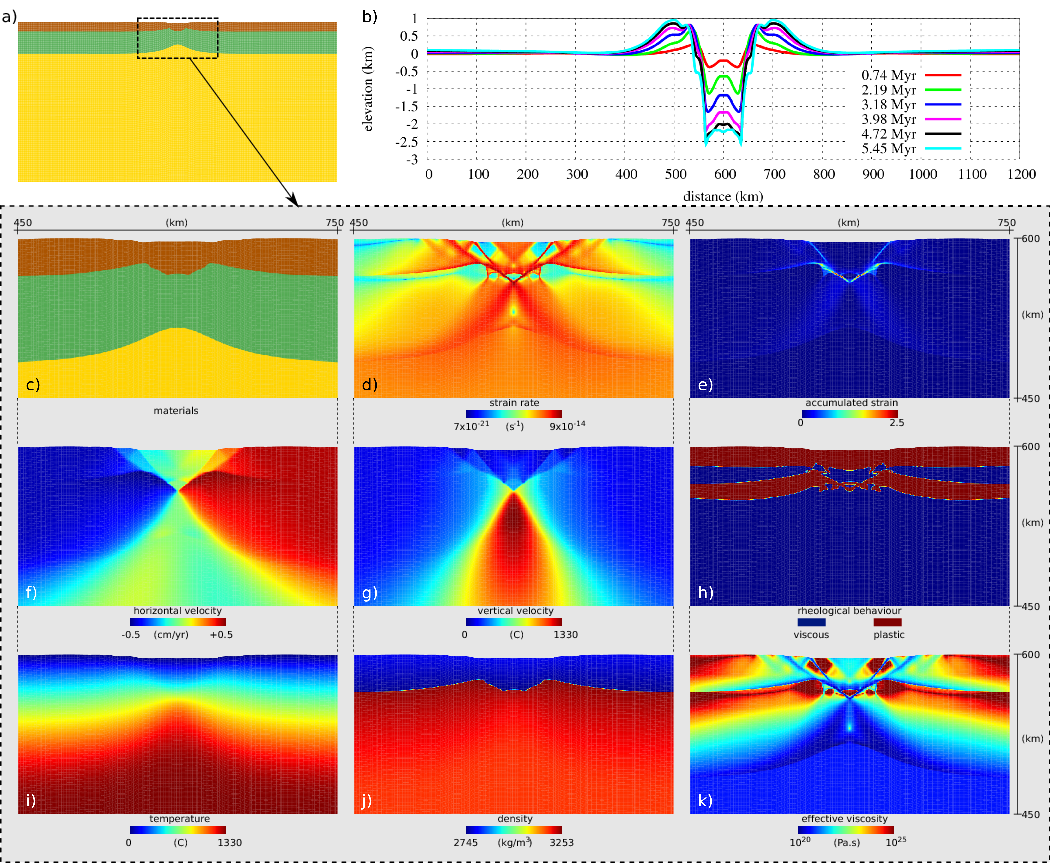
[2] Roles of lithospheric strain softening and heterogeneity in determining the geometry of rifts and continental margins R.S. Huismans and C. Beaumont, Geological Society, London, Special Publications, 282, 2007.

FANTOM3Dp

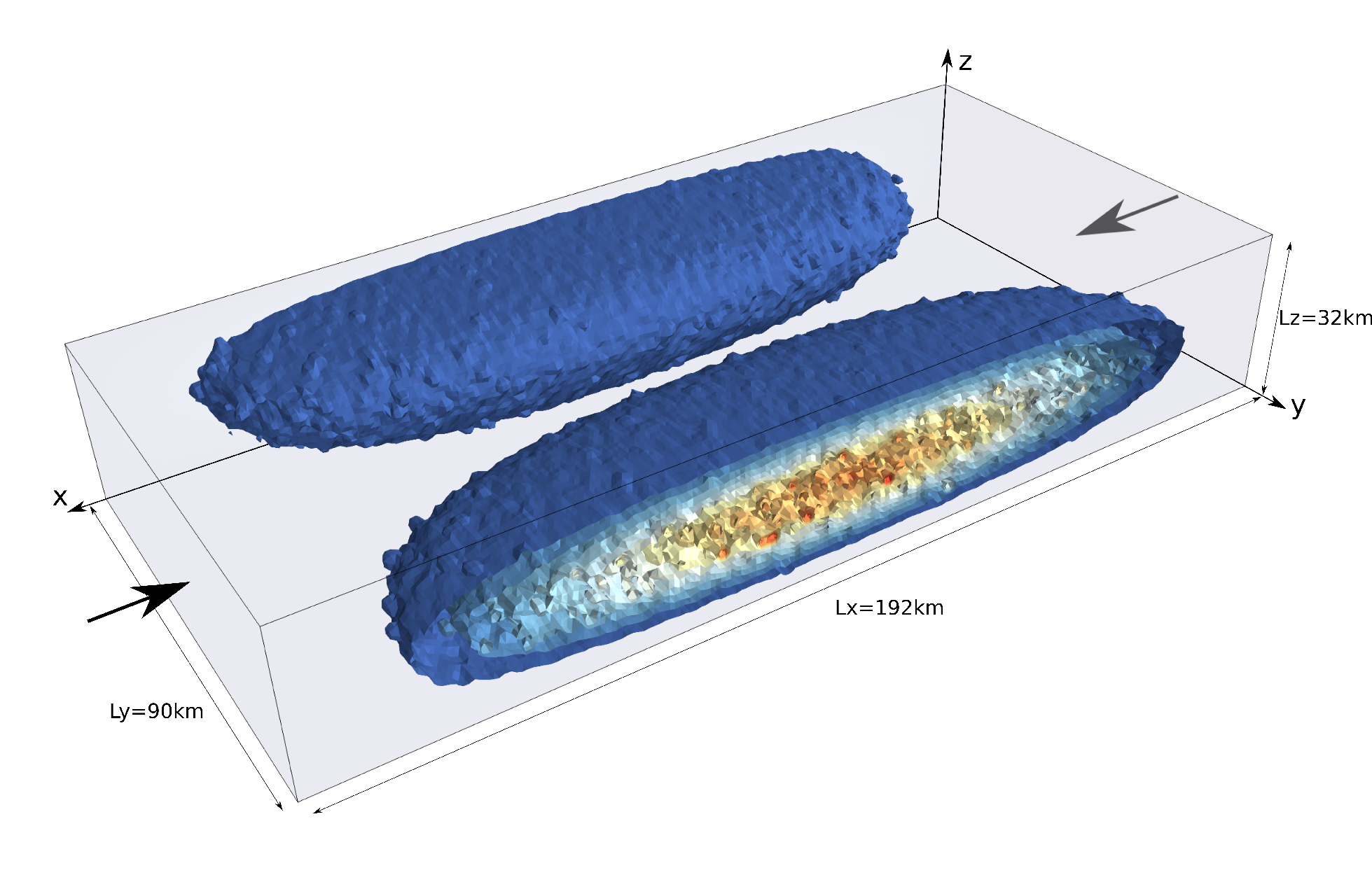
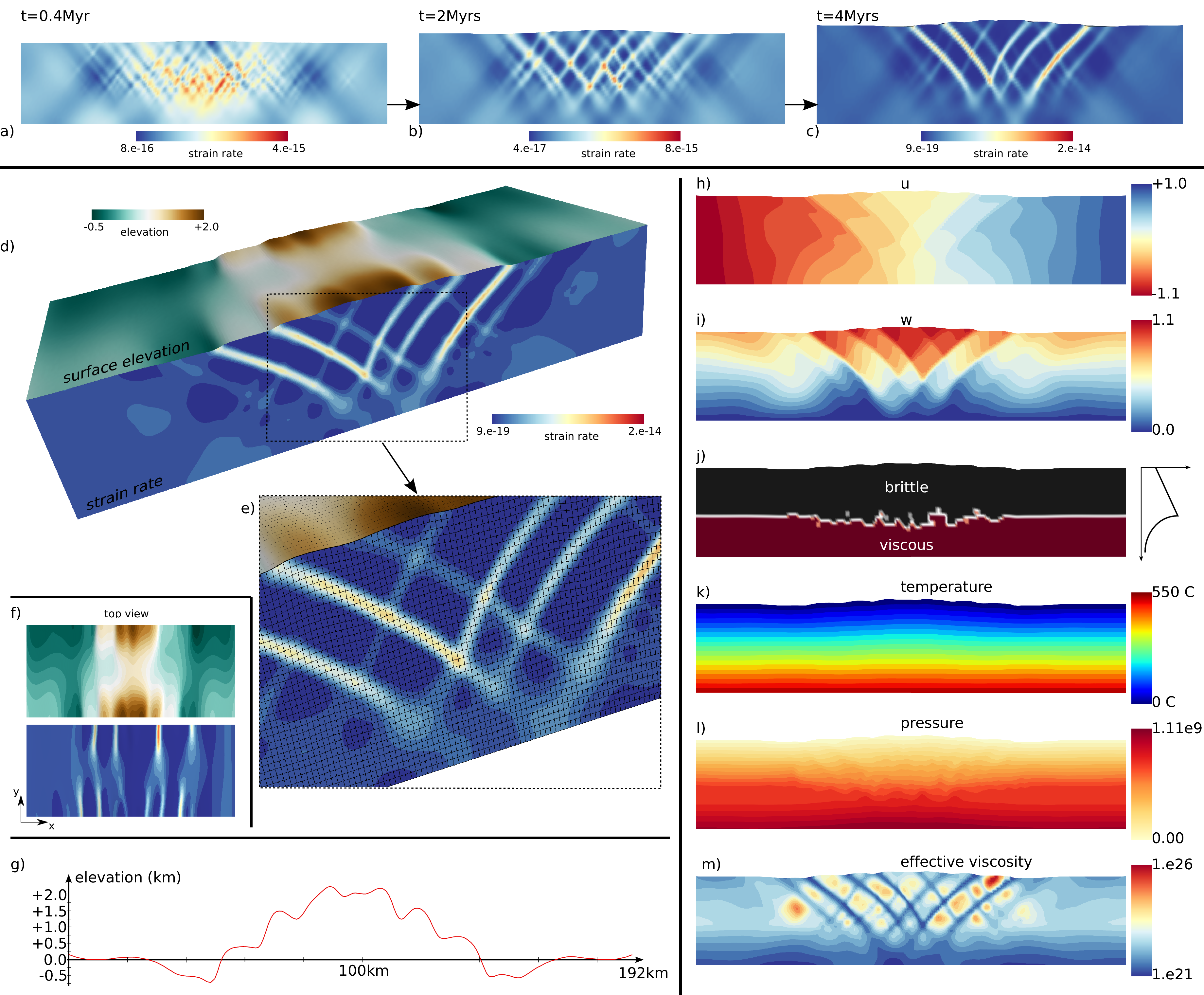
Let us consider a three-dimensional domain of dimensions Lx x Ly x Lz, filled with the same wet quartz which constituted the crust of the previous experiment. It is submitted to compressive velocity boundary conditions: u=+0.5cm/yr on face x=0 and u=-0.5cm/yr on face x=L_x, while v=0 is imposed on both faces y=0 and y=Ly and w=0 is imposed at the bottom of the box.