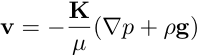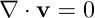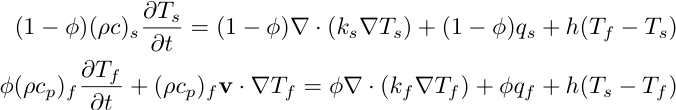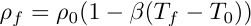Introduction
WAFLE is a simple finite element code which solves the mass, momentum and heat transfer equations in two dimensions in a porous media.
This work was carried out by M. Saltnes (Master student at the Dept. of Mathematics, University of Bergen) and myself between September 2009 and May 2010. The title of the thesis is "Finite Element Modelling for Buoyancy Driven Flow in Natural Geothermal Systems".
The equations under consideration are the following:
- Darcy's law:
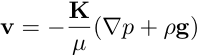
- mass conservation (incompressibility condition):
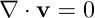
- heat transport:
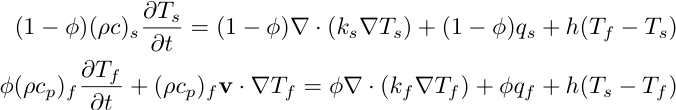
- equation of state:
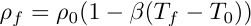
where the subscript f stands for "fluid", and the subscript s for "solid". p is the pressure, g is the gravitational acceleration, phi is the porosity, K the permeability tensor, rho the mass density, T the temperature, h the coefficient of heat transfer between solid and fluid, beta the coefficient of thermal expansion, k the heat conductivity, c_p the heat capacity, and mu the dynamic velocity.
The equations are solved in dimensionless form. Quadrilateral linear finite elements are used. The main features of the code are listed hereunder:
two energy eqs, one for solid and one for fluid: can solve for systems where the temperature of the solid differs from the fluid temperature
porosity can vary in space to account for fractures
the permeability term is a tensor, which allows for the case of anisotropic materials.
periodic boundary conditions can be toggled on/off
Neumann boundary conditions in the heat transport case allow for presence of injection and prodution wells.
built-in grapics and ASCII-output
portable code (a free f90 compiler suffices)
possibility to include more than two materials
built-in scaling
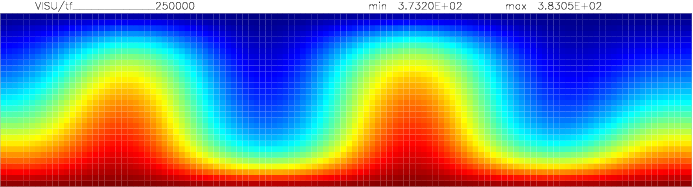
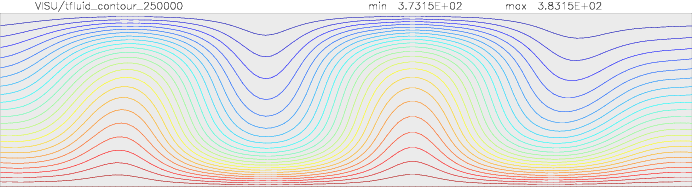
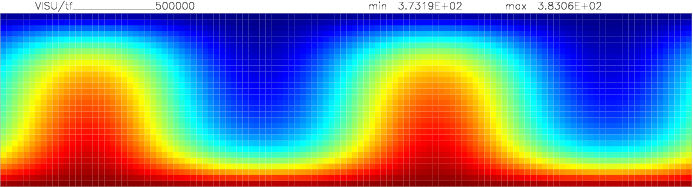
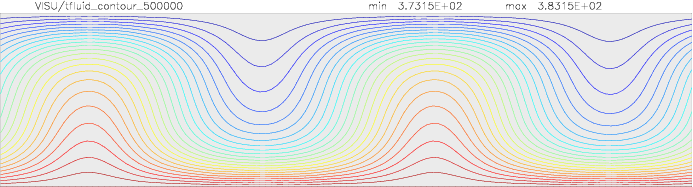
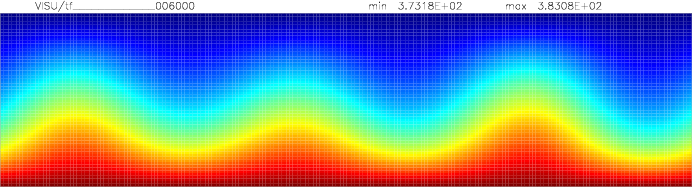
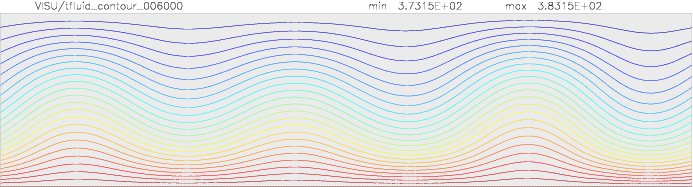
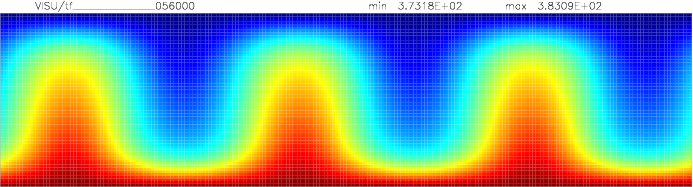
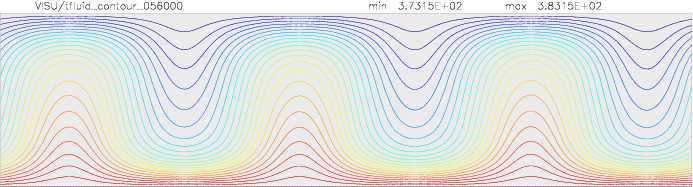
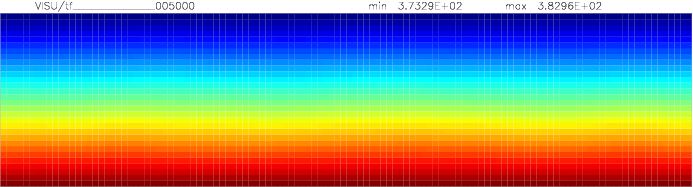
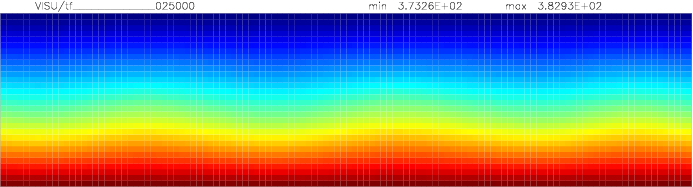
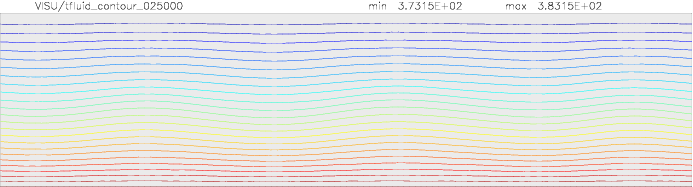
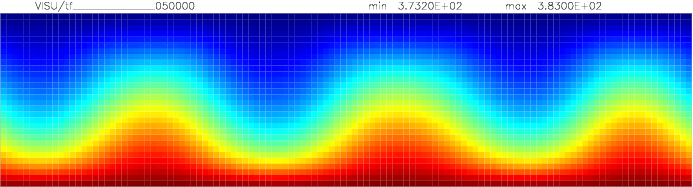
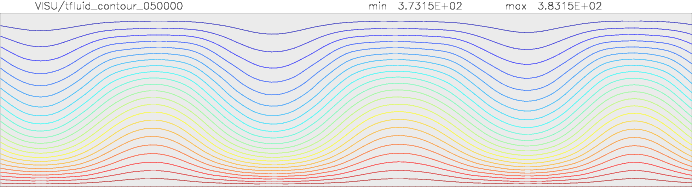
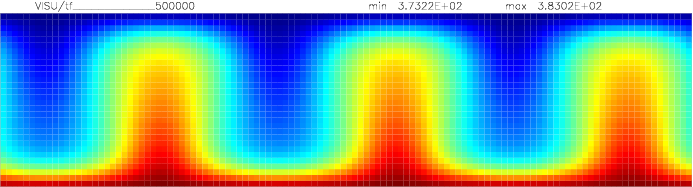
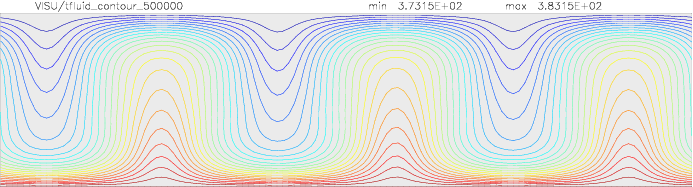
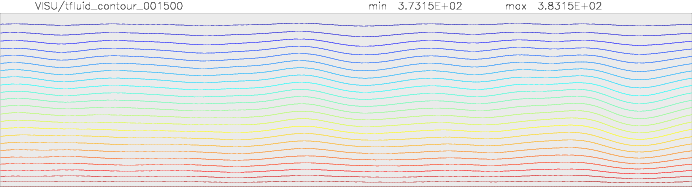
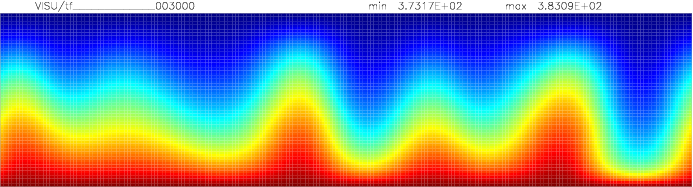
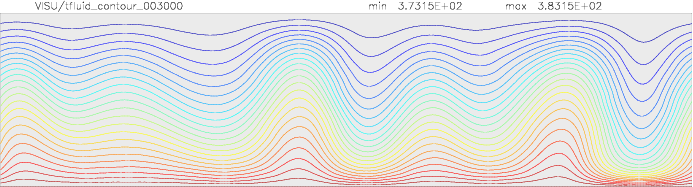
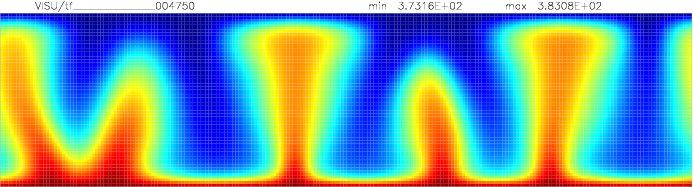
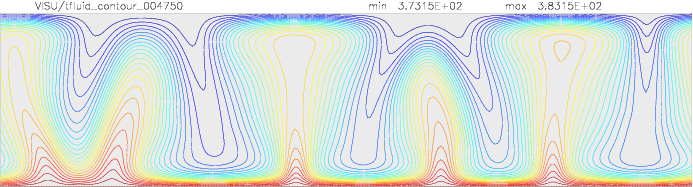
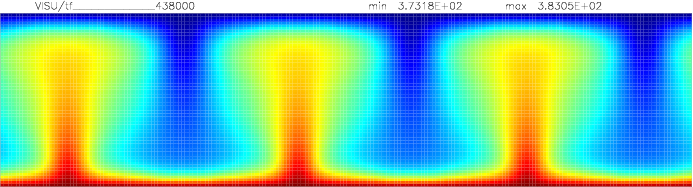
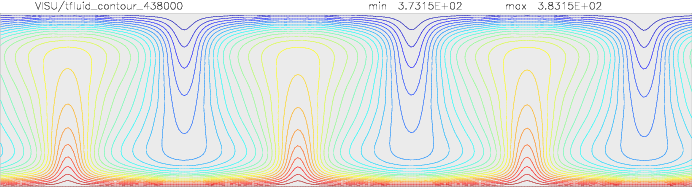
Onset of Darcy-Benard convection
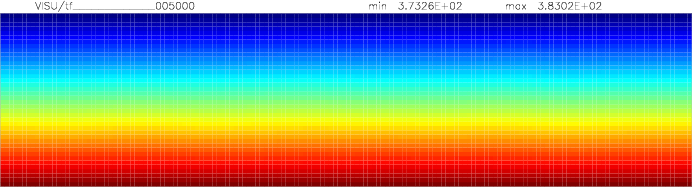
Let us consider a system heated from below and cooled from the top.
We employ a grid consisting of 200×50 elements and horizontal periodic boundary conditions are imposed.
The temperature at the top Tt, is set to 100C, while the temperature at the bottom of the domain is
higher, Tb=110C. The initial temperature field in the system is defined as a linear
gradient between Tb and Tt with a randomness of 1% to trigger the instabilities
needed for convection to occur.